:s historia

- 500 e. Kr.
  ca 2000 f. Kr

Babylonierna använder 3 1/8, dvs 3,125
  1650 f. Kr.

Rhindpapyrusen
"Skär av 1/9 av en diametern och låt resten av diametern bli sida i en kvadrat. Denna har samma area som cirkeln."
Det ger värdet 3 13/81, dvs. 3,16049...
  200-talet f. Kr

Arkimedes använder en omskriven och en inskriven 96-hörning för att bestämma .
Värdet ligger mellan 3 10/71 och 3 1/7, vilket ger medel-
värdet 3,1418..
  100-talet f. Kr K. Ptolemaios anger värdet till 3 17/120= 3,14166...
  400-talet e. Kr. Kinesen Tsu Ch´ung-chih och hans son Tsu Keng-chih använder om- och inskrivna 24576-hörningar!
Det ger närmevärdet 3 16/113, dvs. 3,1415929.
Ingen skulle hitta ett bättre närmevärde på över 1000 år!

1500 - 1800 e. Kr.
1593  F. Viète beskriver som en oändlig produkt: ...
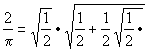1596  Ludolph van Ceulen beräknar med 32 decimaler (35 decimaler år 1610). Han använde Arkimedes metod på polygoner med drygt 20 miljoner sidor.
1600-talet  W. Snell och senare C. Huygens förfinar Arkimedes metod och når häpnadsväckande bra resultat genom att använda om- och inskrivna sexhörningar!!
I Huygens närmevärde var de nio första decimalerna korrekta.
1655  John Wallis använder en integralliknande metod och får fram att ...
  1600-talet  Berömda vetenskapsmän som t.ex. Leibniz och Newton ger viktiga bidrag till metoden att uttrycka som en oändlig serie.
  1706  John Machin beräknar med 100 decimaler.
  1700-talet  L. Euler anger flera effektiva oändliga serier för att beräkna .
  1794  A.M. Legendre bevisar att är irrationellt.
 
  1855 Richter beräknar   med 500 decimaler.
1882 F. von Lindemann bevisar att är transcendent, dvs. kan inte vara en rot till en algebraisk ekvation med heltalskoefficienter.

1901- 1947 e. Kr.
  1947 D. F. Ferguson beräknar med en bordsräknare 808 decimaler. Beräkningen tog ett år!

1949 e. Kr. -  
Datorerna revolutionerar jakten på :s decimaler, men förutom kraftfulla datorer krävs det alltid snillrika matematiker, som hittar effektiva beräkningsmetoder.
1949 Datamaskinen ENIAC beräknar med 2037 decimaler på 70 timmar.
1961  D. Shanks och J. Wrench beräknar med 100 200 decimaler på mindre än nio timmar.
1970-talet Nya algoritmer, lämpade för datorberäkningar, introduceras.
1973 J. Guilloud och M. Bouyer beräknar en miljon decimaler på 23 timmar.
1988 Y. Kanada beräknar över 200 miljoner decimaler på sex timmar.
1996 Bröderna Chudnovsky beräknar en miljard decimaler.
(Genier som dessutom har byggt sina egna superdatorer!)
  1999  Rekord: med 206 158 430 000 decimaler.
  På 2000-talet har rekorden avlöst varandra. Enligt tidningen Ny Teknik var rekordet 2011 10 000 000 000 050 decimaler. Det sattes med hjälp av en dator som den japanska systemingenjören Shigeru Kondo själv byggt ihop. Även programmet som användes för beräkningen är hemsnickrat, av den amerikanska datorforskaren Alexander Yee. Det tog ett år och 6 dagar att göra beräkningen! Elräkningen landade på 31 600 kr.
  2016: Rekord: med 22 500 000 000 000